- Get link
- X
- Other Apps
Propriedades ondulatórias das partículas no sistema categorial Graceli.
quinta-feira, 22 de novembro de 2018
Equação de Schrödinger no sistema categorial Graceli.
Equação de Schrödinger Dependente do Tempo (geral)

 ,
,

Equação de Schrödinger Dependente do Tempo (geral)

x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
 ,
,x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl

x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Equação dependente do tempo[editar | editar código-fonte]
Usando a notação de Dirac, o vetor de estados é dado, em um instante  por
por  . A equação de Schrödinger dependente do tempo, então, escreve-se:[5]
. A equação de Schrödinger dependente do tempo, então, escreve-se:[5]
 por
por  . A equação de Schrödinger dependente do tempo, então, escreve-se:[5]
. A equação de Schrödinger dependente do tempo, então, escreve-se:[5]Equação de Schrödinger Dependente do Tempo (geral)
Em que  é a unidade imaginária,
é a unidade imaginária,  é a constante de Planck dividida por
é a constante de Planck dividida por  , e o Hamiltoniano
, e o Hamiltoniano  é um operador auto-adjunto atuando no vetor de estados. O Hamiltoniano representa a energia total do sistema. Assim como a força na segunda Lei de Newton, ele não é definido pela equação e deve ser determinado pelas propriedades físicas do sistema.
é um operador auto-adjunto atuando no vetor de estados. O Hamiltoniano representa a energia total do sistema. Assim como a força na segunda Lei de Newton, ele não é definido pela equação e deve ser determinado pelas propriedades físicas do sistema.
 é a unidade imaginária,
é a unidade imaginária,  é a constante de Planck dividida por
é a constante de Planck dividida por  , e o Hamiltoniano
, e o Hamiltoniano  é um operador auto-adjunto atuando no vetor de estados. O Hamiltoniano representa a energia total do sistema. Assim como a força na segunda Lei de Newton, ele não é definido pela equação e deve ser determinado pelas propriedades físicas do sistema.
é um operador auto-adjunto atuando no vetor de estados. O Hamiltoniano representa a energia total do sistema. Assim como a força na segunda Lei de Newton, ele não é definido pela equação e deve ser determinado pelas propriedades físicas do sistema.Equação independente do tempo[editar | editar código-fonte]
Equação unidimensional[editar | editar código-fonte]
Em uma dimensão, a equação de Schrödinger independente do tempo para uma partícula escreve-se:[6]
,
em que  é a função de onda independente do tempo em função da coordenada
é a função de onda independente do tempo em função da coordenada  ;
;  é a constante de Planck
é a constante de Planck  dividida por
dividida por  ;
;  é a massa da partícula;
é a massa da partícula;  é a função energia potencial e
é a função energia potencial e  é a energia do sistema.
é a energia do sistema.
 é a função de onda independente do tempo em função da coordenada
é a função de onda independente do tempo em função da coordenada  ;
;  é a constante de Planck
é a constante de Planck  dividida por
dividida por  ;
;  é a massa da partícula;
é a massa da partícula;  é a função energia potencial e
é a função energia potencial e  é a energia do sistema.
é a energia do sistema.Equação multidimensional[editar | editar código-fonte]
Em mais de uma dimensão a equação de Schrödinger independente do tempo para uma partícula escreve-se:[7]
no sistema categorial Graceli, se tem outros parâmetros para energia, massa, momentum, número quântico, e outros.
onde os valores devem ser submetidos ao sistema categorial Graceli.
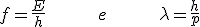
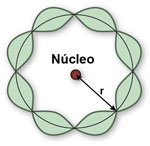
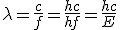
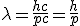
 A Equação de Schrödinger permite calcular a função de onda Ψ (r,t), associada a uma partícula que se move dentro de um campo de forças descrito por um potencial V (r,t). No caso em que o potencial não depende do tempo, ela é expressa do seguinte modo:
A Equação de Schrödinger permite calcular a função de onda Ψ (r,t), associada a uma partícula que se move dentro de um campo de forças descrito por um potencial V (r,t). No caso em que o potencial não depende do tempo, ela é expressa do seguinte modo:
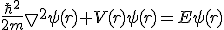
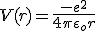 ,
,
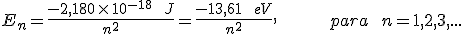

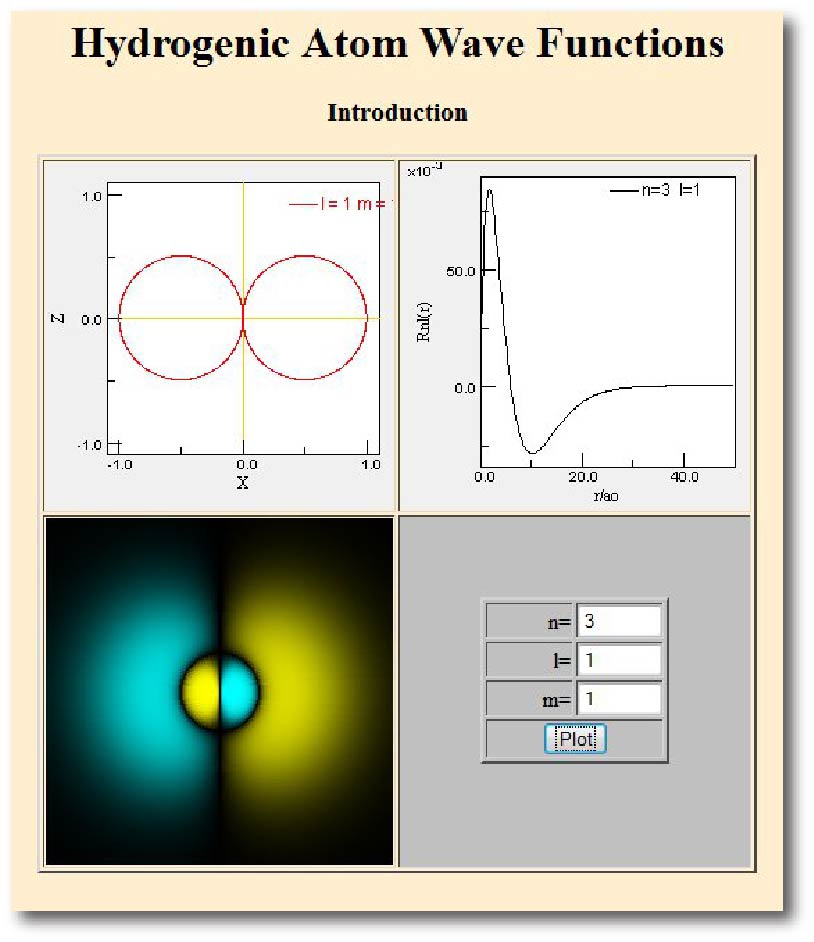
Uma função de onda de um estado quântico do átomo de hidrogênio é identificada com um conjunto (n, l, ml) de números quânticos. O número quântico n determina o nível de energia. O número quântico l é uma medida do módulo do momento angular orbital desse estado quântico. O terceiro número quântico ml está relacionado à orientação no espaço do vetor momento angular.
onde os valores devem ser submetidos ao sistema categorial Graceli.
Matriz categorial de Graceli.
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Tipos, níveis, potenciais, tempo de ação, temperatura, eletricidade, magnetismo, radioatividade, luminescências, dinâmicas, estruturas, fenômenos, transições de fenômenos e estados físicos, e estados de energias, dimensões fenomênicas de Graceli.
trans-intermecânica de supercondutividade no sistema categorial de Graceli.
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
EPG = d [hc] [T / IEEpei [pit] = [pTEMRLD] and [fao] [itd] [iicee] tetdvd [pe] cee [caG].]
p it = potentials of interactions and transformations.
Temperature divided by isotopes and physical states and potential states of energies and isotopes = emissions, random wave fluxes, ion interactions, charges and energies structures, tunnels and entanglements, transformations and decays, vibrations and dilations, electrostatic potential, conductivities, entropies and enthalpies. categories and agents of Graceli.
h e = quantum index and speed of light.
[pTEMRlD] = THERMAL, ELECTRICAL, MAGNETIC, RADIOACTIVE, Luminescence, DYNAMIC POTENTIAL] ..
EPG = GRACELI POTENTIAL STATUS.
[pTFE] = POTENCIAL DE TRANSIÇÕES DE FASES DE ESTADOS FÍSICOS E DE ENERGIAS E FANÔMENOS [TRANSIÇÕES DE GRACELI]
, [pTEMRLD] [hc] [pI] [PF] [pIT][pTFE] [CG].
Propriedades ondulatórias das partículas
Em 1923, o físico francês Louis Victor de Broglie postulou o comportamento ondulatório da matéria:
"Em virtude de os fótons terem características ondulatórias e corpusculares, talvez todas as formas de matéria tenham propriedades ondulatórias e também corpusculares."
Esta foi uma ideia proposta, diferentemente das propostas por Thomson, Rutherford e Bohr, que não tinham evidências experimentais.
Este postulado diz que os elétrons têm também natureza dupla de partícula e onda, sendo acompanhados por uma onda.
Para a frequência f e o comprimento de onda λ da onda, associado ao elétron, ele propôs as equações
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
onde p é o momento e E a energia do elétron.
Note que a primeira equação é a de Planck, E=hf, para o fóton, agora utilizada para o elétron, e que a equação para λ também vale para

fótons e elétrons. Para os fótons temos que
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
Utilizando a relação entre energia e momento da relatividade especial, E=pc, temos:
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
As equações de Louis de Broglie foram propostas para qualquer tipo de matéria. Para corpos macroscópicos, os comprimentos de onda de Broglie são tão pequenos que impossibilitam a sua observação pela interferência ou pela difração. Calcule o comprimento de onda de uma partícula de massa 1g e velocidade 1.000 km/h.
Em 1927, experiências de difração realizadas com elétrons comprovaram as hipóteses de Louis de Broglie.
Função de onda
Com a comprovação experimental da natureza ondulatória das partículas, e estabelecido o seu comprimento de onda 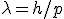 , o próximo passo foi descobrir qual grandeza física está associada à onda de matéria. Nenhuma grandeza física conhecida explica a natureza dessas ondas, então foi utilizada a letra grega Ψ para designar a função de onda da matéria.
, o próximo passo foi descobrir qual grandeza física está associada à onda de matéria. Nenhuma grandeza física conhecida explica a natureza dessas ondas, então foi utilizada a letra grega Ψ para designar a função de onda da matéria.
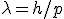 , o próximo passo foi descobrir qual grandeza física está associada à onda de matéria. Nenhuma grandeza física conhecida explica a natureza dessas ondas, então foi utilizada a letra grega Ψ para designar a função de onda da matéria.
, o próximo passo foi descobrir qual grandeza física está associada à onda de matéria. Nenhuma grandeza física conhecida explica a natureza dessas ondas, então foi utilizada a letra grega Ψ para designar a função de onda da matéria.Em 1926, Erwin Schrödinger descobriu uma equação que permite encontrar a função de onda de uma partícula, a partir do conhecimento da energia potencial à qual esta está submetida.
Entretanto foi Max Born que, em 1928, descobriu a relação entre a função de onda e a probabilidade de se encontrar a partícula numa determinada posição. Ele concluiu que 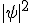 é a grandeza estatística que representa a densidade de probabilidade. Esta função dá a probabilidade de encontrarmos uma partícula numa determinada região do espaço.
é a grandeza estatística que representa a densidade de probabilidade. Esta função dá a probabilidade de encontrarmos uma partícula numa determinada região do espaço.
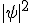 é a grandeza estatística que representa a densidade de probabilidade. Esta função dá a probabilidade de encontrarmos uma partícula numa determinada região do espaço.
é a grandeza estatística que representa a densidade de probabilidade. Esta função dá a probabilidade de encontrarmos uma partícula numa determinada região do espaço.Com esta última descoberta, a Física Quântica mostra que a natureza possui um comportamento estatístico, sendo descrita por uma função que representa a probabilidade. Este fato incomodou muitos físicos, inclusive Einstein, que expressou sua insatisfação dizendo:
- Deus não joga dados com o Universo.
Entretanto os resultados experimentais dão o veredicto a favor da formulação quântica.
Equação de Schrödinger
 A Equação de Schrödinger permite calcular a função de onda Ψ (r,t), associada a uma partícula que se move dentro de um campo de forças descrito por um potencial V (r,t). No caso em que o potencial não depende do tempo, ela é expressa do seguinte modo:
A Equação de Schrödinger permite calcular a função de onda Ψ (r,t), associada a uma partícula que se move dentro de um campo de forças descrito por um potencial V (r,t). No caso em que o potencial não depende do tempo, ela é expressa do seguinte modo:x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
A resolução da Equação de Schrödinger conduz a um conjunto de funções de onda e a um conjunto de energias correspondentes aos estados do elétron permitidos no átomo. As expressões matemáticas das funções de onda possibilitam determinar a probabilidade de encontrar o elétron na vizinhança de um ponto próximo do núcleo.
No caso do átomo de hidrogênio, a energia potencial eletrostática é dada por
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
onde e é a carga elementar, εo é a constante elétrica de permissividade no vácuo e r é a distância ao centro do átomo. Este é um potencial no espaço tridimensional.
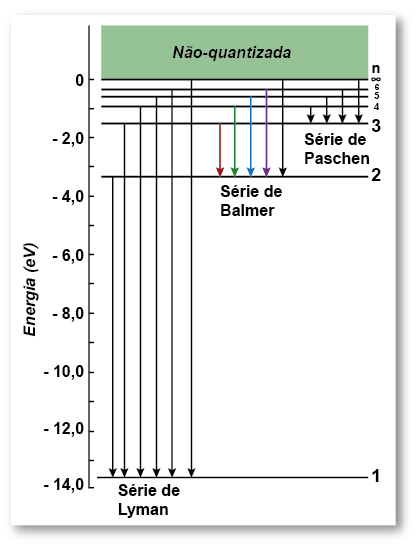
Energias do hidrogênio
A solução da Equação de Schrödinger para este potencial, que não apresentarei aqui, mostra que os valores de energia são quantizados, e são os mesmos obtidos pelo modelo de Bohr.
x
T l T l E l Fl dfG l
N l El tf l
P l Ml tfefel
Ta l Rl
Ll
Dl
| (Clique na imagem para ampliá-la) |
O nível n=1 é o estado fundamental, os outros níveis são estados excitados. O elétron pode receber energia e subir para um desses estados, mas depois de um curto intervalo de tempo volta para o estado fundamental.
Se o elétron estiver no nível fundamental e receber uma energia de pelo menos 13,61 eV, é arrancado do átomo. Temos, neste caso, um elétron livre e um íon do hidrogênio.
Mais números quânticos
As funções de onda, obtidas a partir da equação de Schrödinger, que descrevem os estados quantizados do átomo de hidrogênio, exigem três números quânticos, correspondentes às três dimensões em que o elétron pode se mover.
Números quânticos do átomo de hidrogênio
Utilize esta simulação (clique na figura) para ver as funções de onda para diferentes valores de (n, l, ml).
Assinar: Postagens (Atom)
- Get link
- X
- Other Apps



Comments
Post a Comment